10 Crystal Morphology and Symmetry

KEY CONCEPTS

• The external symmetry of a crystal is the geometrical relationship between its faces and edges.
• Crystal symmetry is a reflection of internal atomic arrangement and symmetry.
• If a crystal has symmetry, the symmetry is common to all of its properties.
• By studying crystal symmetry, we can make inferences about internal atomic order.
• Crystals may have any of an infinite number of shapes, but the number of possible symmetries is limited.
• Crystal symmetry is the basis for dividing crystals into different groups and classes.

10.1 Symmetry

10.1.1 Introduction

The shape of a crystal reflects its internal atomic arrangement, and the most important aspect of a crystal’s shape is its symmetry. As defined by the ancient Greek philosopher Aristotle, symmetry refers to the relationship between parts of an entity. Symmetry may be of many sorts. For example, a hexagon has 6-fold symmetry; we can rotate it 60^o six times and get back to where we started. And wallpaper that contains a repeating pattern of some sort has symmetry; the pattern repeats with even spacing vertically and horizontally. Zoltai and Stout (1984) give an excellent practical definition of symmetry as it applies to crystals: “Symmetry is the order in arrangement and orientation of atoms in minerals, and the order in the consequent distribution of mineral properties.”

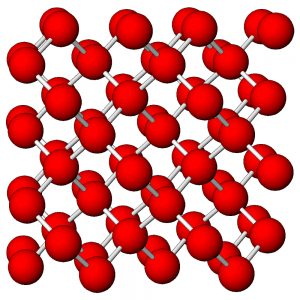
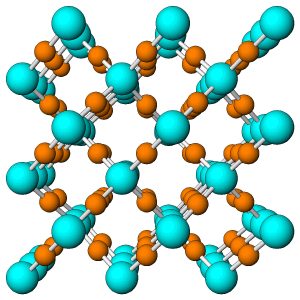
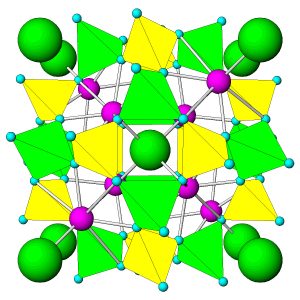
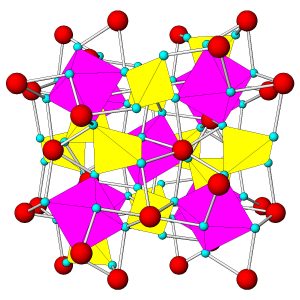
Figure 7.54 (Chapter 7) showed the atomic arrangement in halite. Halite, like all minerals, is built of fundamental building blocks called unit cells. In halite crystals, the unit cells have a cubic shape. Fluorite, too (Figure 7.55, Chapter 7) has a cubic unit cell. Figures 10.2, 10.3, 10.4, and 10.5, below, show other minerals with an overall cubic arrangement of their atoms. Diamond’s atomic arrangement is quite simple because it only contains carbon. Cuprite is a bit more complicated because copper and oxygen atoms alternate. Sodalite and garnet are even more complicated. But, all these minerals have cubic unit cells. The unit cells have what is called cubic symmetry.

blank
Unit cells may have any of six fundamental shapes with different symmetries. Cubic unit cells, which have the most symmetry possible, may stack together to produce an irregularly shaped crystal that displays no symmetry. But, they may also stack together to create crystals with six identical faces at 90^o to each other (a cube). Minerals with shoe-box shaped unit cells, in contrast, cannot form cubic crystals. And, as we will see, unit cells with less symmetry (that are neither cubic nor shoe-box shaped) cannot combine to form crystals that are cubic or crystals that are shoe-box shaped. So, the symmetry of the unit cell limits possible crystal symmetry.

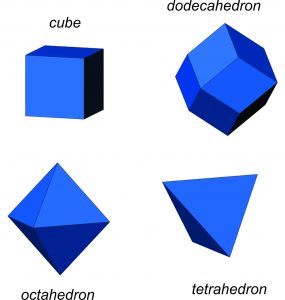
Although the relationship between a cubic arrangement of atoms and a cube-shaped crystal may seem clear, things are not always so simple. Halite has a cubic unit cell, and euhedral halite crystals are generally cubes like the one shown in Figure 10.6. And, cuprite crystals (Figure 10.3) may be cubes, too, but they are also sometimes octahedra (Figure 10.6). Notice that octahedra are equivalent to cubes with their corners removed and replaced with crystal faces. Cubes and octahedra, and also dodecahedra and tetrahedra (Figure 10.6) are all closely related because they are made of cubic unit cells, and the atomic arrangement in each is the same in three perpendicular directions.

Sodalite (Figure 10.4) and garnet (Figure 10.5) both have cubic unit cells but typically form rhombic dodecahedral crystals. (There are different kinds of dodecahedra but for brevity, when we refer to a dodecahedron in the rest of this chapter we are talking about a rhombic dodecahedron, such as the one seen in Figure 10.6.) And, diamond (Figure 10.2) crystals may be octahedra, dodecahedra, cubes, and tetrahedra. Figure 10.6 shows those possible crystal shapes. These crystals all look different, and have different numbers of faces, yet all of these have the same shaped (cubic) unit cells.

So, we see that if the atomic arrangement has cubic symmetry, a crystal may or may not be cubic. And, it may or may not have the same symmetry as a cube. But, we can turn this around. If a crystal shows some kind of symmetry, the atoms within it must be arranged with at least that much symmetry. They may have more. For example, as we will see later in this chapter, crystals of many different shapes must have cubic atomic arrangements, even though the crystals are not cubes. Thus, the external symmetry of a crystal tells us about the atomic arrangement within. In this chapter, the focus is on crystal symmetry. In the following chapter we will look more closely at the atomic arrangements implied by that symmetry.

For an introduction to the different types of symmetry that crystals may have, watch the video linked below:
blank▶️ Video 10-1: Symmetry of crystals (4 minutes)

10.1.2 Identifying Symmetry

Looking for symmetry in natural materials can be complicated. Although atomic arrangements may be symmetrical, many things control crystal growth, so crystal shapes may not reflect their internal order. Sometimes few or no crystal faces may form. Sometimes several different crystals become intergrown. Sometimes crystals contain structural imperfections. Some crystals have pseudosymmetry, which means they appear to have certain symmetry but, if you could look closer or make precise measurements, you would find that they do not. And, other crystals may be too small to see clearly. An experienced eye and an active imagination are often necessary to see the symmetry of natural mineral crystals.

10.1.3 Mirror Planes

Most animals, including humans and lions (Figure 10.7), appear symmetrical: an imaginary mirror down their center relates the appearance of their right side to their left side. We call such symmetry reflection, and we call the plane of the imaginary mirror the mirror plane. In shorthand notation, we use the letter m to designate a mirror of symmetry. Reflection is the symmetry operation, and the mirror plane is the symmetry operator. Reflection often relates identical faces on a crystal. Figure 10.8a shows a butterfly that has the same symmetry as a lion.

A face, or any object, on one side of a mirror has an equivalent at an equal distance on the other side of the mirror. The two faces or objects are the same perpendicular distance from the mirror and have opposite handedness, like your two hands shown in Figure 10.8b (one has the thumb on the left side and the other has the thumb on the right side).

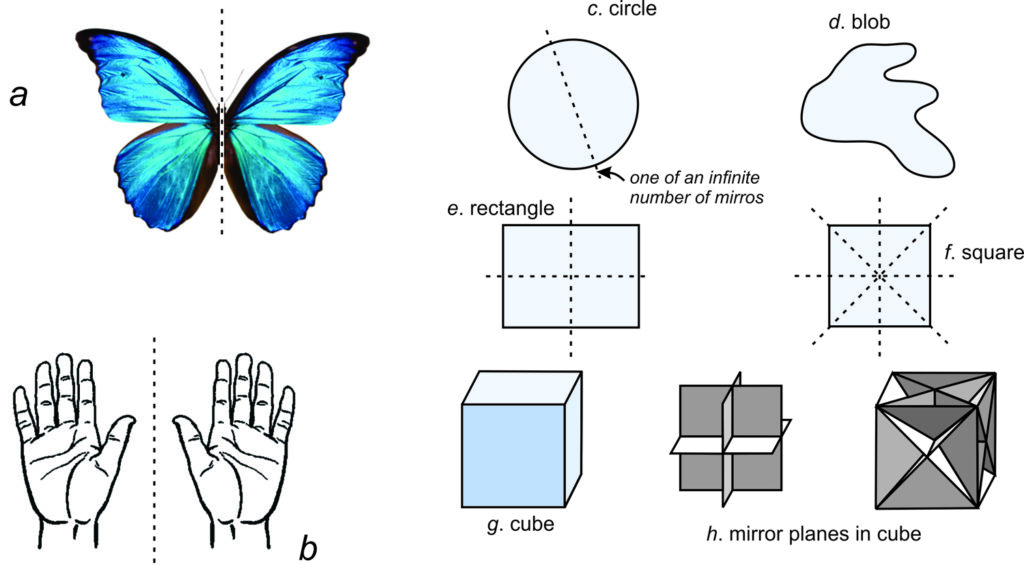
Two-dimensional drawings may have many mirror planes or no mirror planes. A circle (Figure 10.8c), for example, contains an infinite number of mirror planes; any line drawn through the center of the circle is a mirror of symmetry. Irregular blobs (Figure 10.8d), on the other hand, have no mirror planes. A rectangle (Figure 10.8e) contains two mirror planes, while squares (Figure 10.8f) have four. Box 10-1 contains more examples of mirror planes in 2D.

Three-dimensional objects, too, may have zero to many mirror planes. A cube (Figure 10.8g) has nine mirrors. Three are parallel to pairs of opposite faces; six intersect opposite faces along their diagonals (Figure 10.8h). Thus, a cube has more symmetry than a human, a lion, or a butterfly. (A perfect sphere has an infinite number of mirror planes, but, as we will see later, crystals cannot have more mirror planes than a cube.)

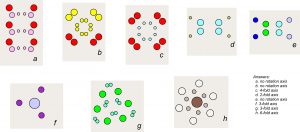
● Box 10-1 Mirror Planes in 2D The drawings below show colorful patterns. Most of them contain mirror planes. How many mirror planes do you see in each pattern?

For a video with further discussion of mirror planes:
blank▶️ Video 10-2: Mirror planes (6 minutes)

10.1.4 Rotational Symmetry

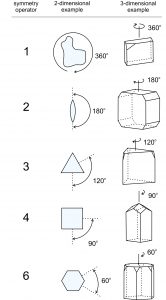
Reflection by a mirror is one of several types of symmetry operations. A second common type of symmetry in crystals, called rotational symmetry, is symmetry with respect to a line called a rotation axis. In two dimensions, a lens shape appears unchanged when rotated 180° (symmetry operator 2 in Figure 10.10). We say it has 2-fold symmetry because two repeats of a 180^o rotation operation return it to its original position. A 2-fold rotation axis is perpendicular to the plane of the page.

Figure 10.10 also shows other rotational symmetry operators. Equilateral triangles have 3-fold rotational symmetry. Rotate an equilateral triangle 120° and it appears the same. Do it three times and you are back to where you started.

Squares have 4-fold rotational symmetry (rotation of 90°), and hexagons have 6-fold rotational symmetry (rotation of 60°). Box 10-2 contains more examples of rotation axes in 2D.

The right-hand column in Figure 10.10 shows three-dimensional shapes – they might be crystals – with the different kinds of rotational symmetry (1-fold, 2-fold, 3-fold, 4-fold, and 6-fold). Many of them also contain mirror planes of symmetry. Thus we see that crystals may have more than one kind of symmetry. Fortunately the number of possible combinations is limited, which makes analyzing crystal symmetry easier than it would be otherwise.

All objects have 1-fold rotational symmetry because they remain unchanged after rotation of 360°. This seems trivial, but for completeness we have included 1-fold symmetry in Figure 10.10. And, although we can draw shapes that have 5-fold symmetry, or greater than 6-fold symmetry, minerals never possess such symmetry. For example, some natural materials, including plants and animals such as a starfish (having 5 legs), display apparent symmetries not possible for minerals. We will discuss why in the following chapter.

We call all the rotation axes we have just discussed proper rotation axes, to contrast them with rotoinversion axes, which we will discuss later. In shorthand notation, we symbolize proper rotation axes using the numbers 1, 2, 3, 4, or 6, corresponding to rotations of 360°, 180°, 120°, 90°, and 60°, respectively. The “fold” value tells us how many times the operation has to be repeated to return to the starting position – how many times it takes to add up to 360^o. Sometimes in drawings, we use a small lens shape, a triangle, a square, or a hexagon instead of numbers to show symmetry and label the different rotation axes.

● Box 10-2 Rotation Axes in 2D The drawings below show colorful patterns. Most are the same patterns you saw in the previous box. They all have 1-fold rotational symmetry. What other kinds of rotation axis (2-fold, 3-fold, 4-fold, or 6-fold) do you see in each drawing? (Some contain none.)

Above, we noted that cubes have nine mirror planes. Cubes also have 2-fold, 3-fold, and 4-fold rotational symmetry, shown in Figure 10.12. When rotated 180° about an edge diagonal, a cube appears unchanged drawing on left). When rotated 120° about a main diagonal (drawing in the center), or when rotated 90° about a line perpendicular to a face (drawing on the right), a cube does not change. Thus, we see that different rotation axes can combine in crystals. Cubes, with all their mirror planes and rotation axes, have the most symmetry possible for a crystal.

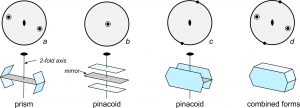
Many minerals grow as prisms, crystals having a set of identical faces parallel to one direction. Typically, prismatic crystals are elongated in one direction. Figure 10.13 shows a green prismatic crystal of apophyllite, a zeolite. The crystal has four vertical faces and a square cross section. It also has sloping terminating faces at the top and bottom ends. Figure 10.14 shows a hexagonal prism of apatite. The prism has six sides – all parallel to one direction – and terminating faces on its top. If the crystal was perfectly formed, there would also be six terminating faces on the bottom.

Prism faces are, in principle, identical in shape and size, although accidents of growth often lead to minor differences. Some minerals have multiple, nonidentically-shaped faces, all parallel to a common line. We call the collection of faces a zone and the common line the zone axis. Zones, present in most crystals, sometimes correspond to rotational axes of symmetry.

Symmetry can be enigmatic. For example, anhedral crystals exhibit no external symmetry, while euhedral crystals may exhibit a lot. And, rotational symmetry, even if present, may be hard to see. For example, the 3-fold axes of symmetry in a cube are difficult to see without turning the cube in your hand. Problems may be even more complicated in natural crystals because of growth imperfections in crystal faces, or the presence of many differently shaped crystal faces.

10.1.5 Inversion Centers

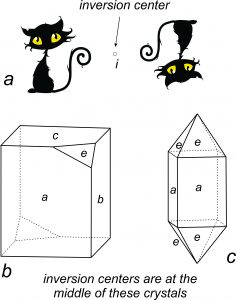
We just looked at reflection and rotation, two kinds of symmetry. Inversion, a third type of symmetry, is symmetry with respect to a point. We call the point the inversion center and often designate it with the lowercase letter i. As with mirror planes, inversion relates identical faces on a crystal. But, while mirror planes “reflect” faces and change their “handedness,” inversion centers invert them.

Inversion produces faces related in the same way that a lens may yield an upside-down and backward image. So, the two cats in Figure 10.15a are related by inversion – they are upside down and backward images of each other. In two dimensions, inversion centers give the same results as 2-fold axes of symmetry. For example, in Figure 10.15a, a cat has been inverted. The cat could have been rotated 180^o and the result would have been the same.

In three dimensions, inversion symmetry is different from rotation. The crystal in Figure 10.15b has an inversion center and no other symmetry. It does not have any rotational symmetry or reflection (mirror plane) symmetry. It contains four different shaped faces (a, b, c, and e); each of them has an inverted matching face on the back and left sides of the crystal. That is all they symmetry that is present.

In contrast, the crystal in Figure 10.15c contains an inversion center, but other symmetry is present, too. 90^o rotation relates the four a-faces. Inversion and rotation relate the eight e-faces. Additionally, many mirror planes are present.

We use small letters on crystal faces, such as those seen in these two crystal drawings, to distinguish faces of different shapes and to show those related by symmetry. The a-faces in Figure 10.15c, for example, are the same shape and are related by a 4-fold rotation axis. Conventions, not worth discussing here, dictate which letters we use for different kinds of faces.

For a video discussion of inversion centers, click on the link below:
blank▶️ Video 10-3: Inversion centers (6 minutes)

10.1.6 Symmetry Operates on Everything

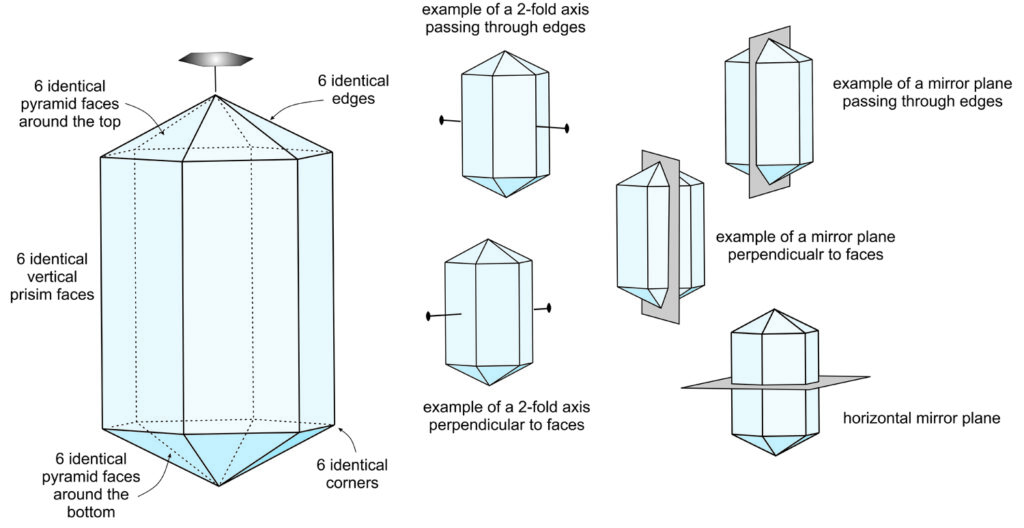
The crystal shown above in Figure 10.16 has a vertical 6-fold axis of symmetry. It has six identical prism faces and six identical pyramid faces on both the top and on bottom. It also has six identical edges around the prism faces and around the pyramid faces.

The crystal has six 2-fold rotation axes that pass through edges, and six other 2-fold axes that are perpendicular to the prism faces. The small insets in Figure 10.16 show one example of each, but five others are identical. Six vertical mirror planes pass through the edges of prism faces, and six other mirrors are perpendicular to the prism faces. The figure shows examples of each. The crystal also has a single horizontal mirror plane through its equator. So, symmetry operates on symmetry – there are six of everything (except the horizontal mirror because it is perpendicular to the 6-fold axis). This crystal also has an inversion center.

This crystal must also have six directions of identical atomic structure and, therefore, six directions with the same hardness, reflectivity, optical properties, and so on. The 6-fold rotation axis affects everything in a crystal, including faces, edges, corners, other symmetry elements, physical properties, optical properties, and atomic arrangement.

10.1.7 Symmetry Is a Property

Mineralogists often speak of a crystal’s symmetry elements – the different kinds of symmetry a crystal has – in quantitative terms. We can count mirror planes, rotation axes, and inversion centers. If objects have only a few symmetry elements, we say they have low symmetry. Those that display many have high symmetry. In addition, we say that objects with 6-fold rotation axes have higher symmetry than those with 4-fold, 3-fold, or 2-fold axes, and so on. References to high and low symmetry are necessarily vague because symmetry manifests itself in many different ways.

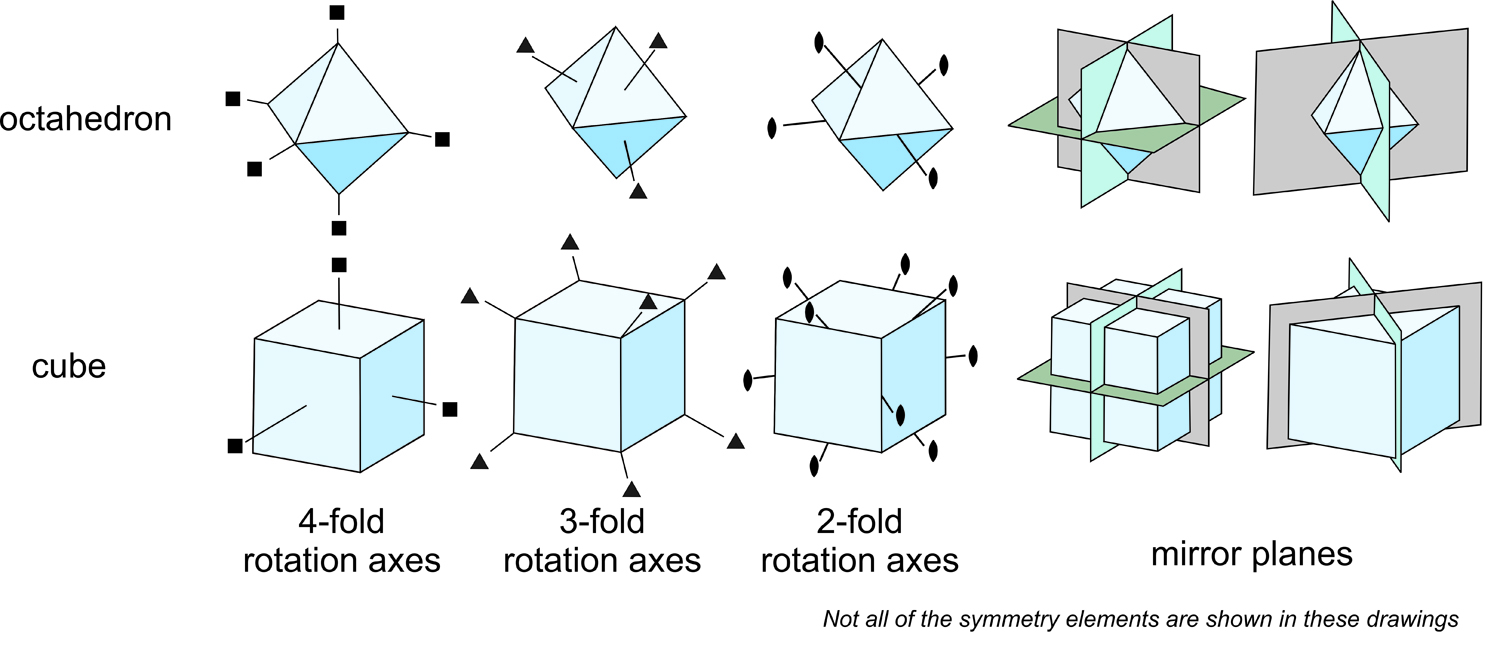
Cubes have the most symmetry possible for crystals: three 4-fold axes, four 3-fold axes, six 2-fold axes, nine mirror planes, and an inversion center. All this symmetry is shown in Figure 10.17. But, octahedra have the same symmetry (also shown in Figure 10.17). Consider the three 4-fold rotation axes. In a cube they are perpendicular to faces. In an octahedron, they come out at the corners. But, in both, these axes are at 90^o to each other. And the four 3-fold axes exit the cube at the corners, but exit the octahedron in the centers of the faces. The 2-fold axes come out of the centers of edges in both crystals. The right side of the figure shows only some of mirror planes because showing them all is too complicated. If you look closely, you will see that the ones shown have identical orientations in both crystals.

A cube has 12 edges, 8 corners and 6 faces. An octahedron has 12 edges, 8 faces and 6 corners. It is as if the faces and corners have switched places. And, both crystals have exactly the same symmetry. Cube faces are at 90^o to each other; octahedron faces are at about 55° to each other, but the mirror planes, rotation axes, and the inversion center are identical for both.

Comparison of the cube and octahedron emphasizes that symmetry is not a physical characteristic. It is a property that objects may possess. With an object in hand, a mineralogist can discuss its symmetry, but a description of an object’s symmetry does not unambiguously reveal its appearance. Many objects have mirror planes, yet their overall shapes are quite different. While symmetry does not determine appearance, it does include all aspects of a crystal.

10.2 Stereo Diagrams

10.2.1 Symmetry on Stereo Diagrams

A convenient way to look at the symmetry of a crystal is to use a stereographic projection, also called a stereo diagram. Stereo diagrams allow us to depict three-dimensional symmetry in a two-dimensional diagram. Although stereo diagrams depict mirror planes, inversion centers, and rotational symmetry, and their relationships to crystal faces, stereo diagrams do not show the shape of faces. The diagrams only show symmetry.

10.2.1.1 Rotation Axes

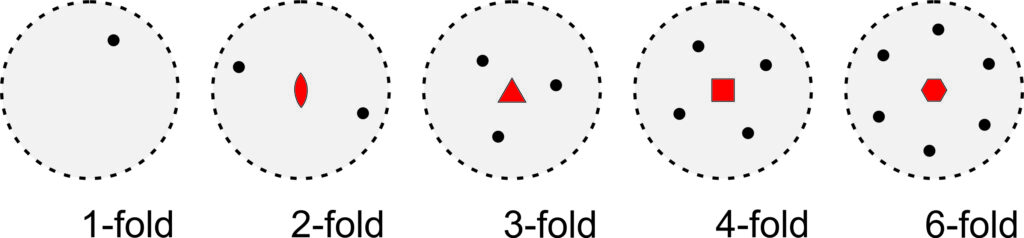
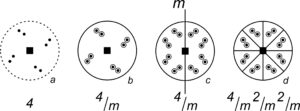
Stereo diagrams can be quantitative and very complex. In this text, considering their qualitative aspects is sufficient. Figure 10.18 shows stereo diagrams depicting 1-fold, 2-fold, 3-fold, 4-fold, and 6-fold rotation axes perpendicular to the page. The geometric symbols (in red) at the center of the diagrams show the kind of rotation axes. In the five drawings, the rotation axis has operated on a single black dot, producing 0, 1, 2, 3, or 5 other dots by rotation of 360°, 180°, 120°, 90°, and 60° around the center of the diagram.

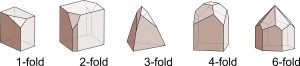
Figure 10.19 shows examples of crystals that have rotation axes. In drawings of this sort, it is often necessary to depict crystals with several differently shaped faces to limit symmetry and make the symmetry clear (as is done in this figure). It is easy to make drawings that have more symmetry than wanted. For example, if the top pyramid faces were not present, the crystals with 2-, 3-, 4-, and 6-fold symmetry would also contain vertical mirrors.

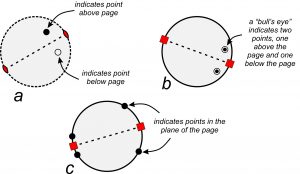
The stereo diagrams in Figure 10.18 show symmetry, and repetition of points, in the plane of the page quite nicely. However, symmetry operations also work in three dimensions. To accommodate the third dimension, we need a way to show points below and above the page. By convention, solid dots represent points above the plane of the page, and circles represent points below the plane of the page (Figure 10.20a). A bull’s-eye symbol, formed by a small circle around a dot, shows a point above the page that is directly above one below the page. Figure 10.20b shows two examples. Points within the plane of the page (around the equator of the crystal) always plot as solid dots on the outside circle of the stereo diagram (Figure 10.20c).

Figure 10.20a and b show a 2-fold and 4-fold axis of symmetry lying in (parallel to) the plane of the page. They operate on points above the page to produce points below. For the 2-fold axis, a black dot (above the page) becomes an open circle (below the page) after a rotation of 180^o around the axis that lies in the plane of the page. The two symbols are not on top of each other. For the 4-fold axis (10.20b), 90^o rotations around the axis (that is in the plane of the page) produce four equivalent points. The two points below the page are directly beneath the two points above, and so are shown as bull’s-eyes.

10.2.1.2 Mirror Planes

In Figure 10.20a, the outside circle is a dashed line. In the other two diagrams it is solid. Why the difference? A solid outside circle indicates that a horizontal mirror plane reflects points above the page to below the page (shown by the bull’s-eye symbol). In contrast, a dashed circle means there is no reflection and no mirror plane parallel to the page. In Figure 10.20c, the points are on the outside and, thus, within the plane of the page, and so cannot reflect up or down. In such cases, the circle could be solid or dashed but is generally shown solid.

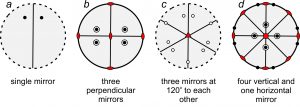
So, mirrors may lie in the plane of the page. They may also have other orientations. For example, the four stereo diagrams in Figure 10.21 include mirror planes that are perpendicular to the page. They appear as straight lines that pass through the centers of the diagrams. Some of these diagrams also depict other kinds of symmetry:

●Diagram a contains a single vertical mirror and two points related by reflection.

●Diagram b contains three mirrors at 90^o to each other – one in the plane of the page (shown by the solid outer circle) and two vertical (shown by straight solid lines). It has a total of eight points – four above the page and four below. This diagram also contains three 2-fold rotation axes, shown by the red lens shapes.

●Diagram c contains three vertical mirrors (straight lines) at 120^o to each other, with nine points (below the page) related by those mirrors. This diagram also contains a 3-fold rotation axis, shown by the red triangle at the diagram’s center.

●Diagram d has a horizontal mirror in the plane of the page (solid circle) and four other vertical mirrors (straight lines). It contains sixteen points related by the symmetry. This diagram also contains four 2-fold axes (lens shapes) and a 4-fold rotation axis (shown by the red square at the diagram’s center).

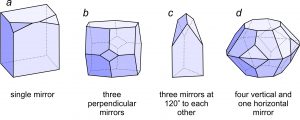
Figure 10.22 shows crystals with symmetries that match the four stereo diagrams in Figure 10.21. Crystal a has only a single mirror plane of symmetry. The right side reflects to the left side. Crystal b has three perpendicular mirror planes and three 2-fold axes. Each 2-fold axis is perpendicular to one of the mirrors. Crystal c has three mirrors that intersect at 120^o this requires that a vertical 3-fold axis be present. Crystal d has four vertical and one horizontal mirror. It also contains four horizontal 2-fold axes and a vertical 4-fold axis.

10.2.1.3 Rotation Axes with Perpendicular Mirror Planes

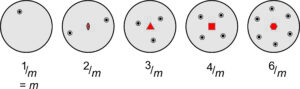
Many crystals, including some depicted in Figure 10.22, contain rotation axes that are perpendicular to mirror planes. Crystallographers use shorthand symbols to describe such combinations. We represent them by the symbols ¹/_m, ²/_m, ³/_m, ⁴/_m, and ⁶/_m. Figure 10.23 shows stereo diagrams for each. In these drawings, the mirror is horizontal and the rotation axis is vertical (perpendicular to the page). Note that the outer circles are solid in all these diagrams, because points above the page are reflected by a horizontal mirror to below the page. The symbol ¹/_m is somewhat redundant because the 1-fold rotation axis changes nothing. So, this symmetry is commonly just signified by m.

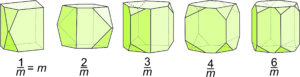
The crystal drawings in Figure 10.24 show crystals with symmetry equivalent to what we see in Figure 10.23. In all drawings, the top faces reflect to the bottom. Note that if these crystals did not have smallish scalene triangular faces, they would appear to have symmetry that included vertical mirror planes. They would look like simple prisms. These crystal shapes reinforce the idea that multiple faces with different shapes are sometimes needed to depict complex symmetry.

10.2.1.4 Rotoinversion Axes

In the discussions above, we talked about reflection, rotation, and inversion operations. Rotoinversion is a fourth, and an important, kind of symmetry operation. Rotoinversion, a combination of rotation and inversion, is a symmetry operation sometimes distinct from the others. The symbols 1, 2, 3, 4, and 6, represent rotoinversion axes. They are articulated as “bar-1,” “bar-2,” etc.

In a rotoinversion operation, we apply rotation and inversion sequentially. Just as with proper rotation axes, the angle of rotation is 360̊^o for a 1-fold rotoinversion axis, 180̊^o for a 2-fold rotoinversion axis, 120^o for a 3-fold rotoinversion axis, etc. (table below.) The difference is that for rotoinversion, rotation of a point is followed by inverting it through the center of a diagram.

rotoinversion axis	1	2	3	4	6
rotoinversion operation	rotate 360̊ and invert	rotate 180̊ and invert	rotate 120̊ and invert	rotate 90̊ and invert	rotate 60̊ and invert

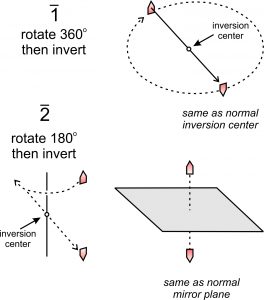
Figure 10.25 shows 1 and 2 rotoinversion operations applied to a single house-shaped motif. The 1 operation involves 360^o rotation followed by inversion. This is the same as a normal inversion center.

The 2 operation involves 180^o rotation followed by inversion. This is the same as reflection by a mirror plane. We include 1 and 2 operations in our list for completeness but recognize that they are redundant.

3 rotoinversion, however, is not so trivial. For example, in Figure 10.26 (below), we apply a 3 axis to solid point 1 (above the page). Rotation of 120^o and inversion produces an open point (point 2, below the page). We repeat the operation: point 2 is rotated 120^o and inverted to produce point 3, and so forth. After five repeats, we have produced points 2, 3, 4, 5, and 6, and we are done because a sixth repeat gets us back to the original point. A 3 axis relates six points in total, shown in the large stereo diagram in the Figure. Examination of this diagram reveals that a 3 axis is the same as a 3-fold axis and an inversion center operating independently. Three of the points are above the page and three below. Those above are not directly above those below – they are offset by a rotation of 60^o.

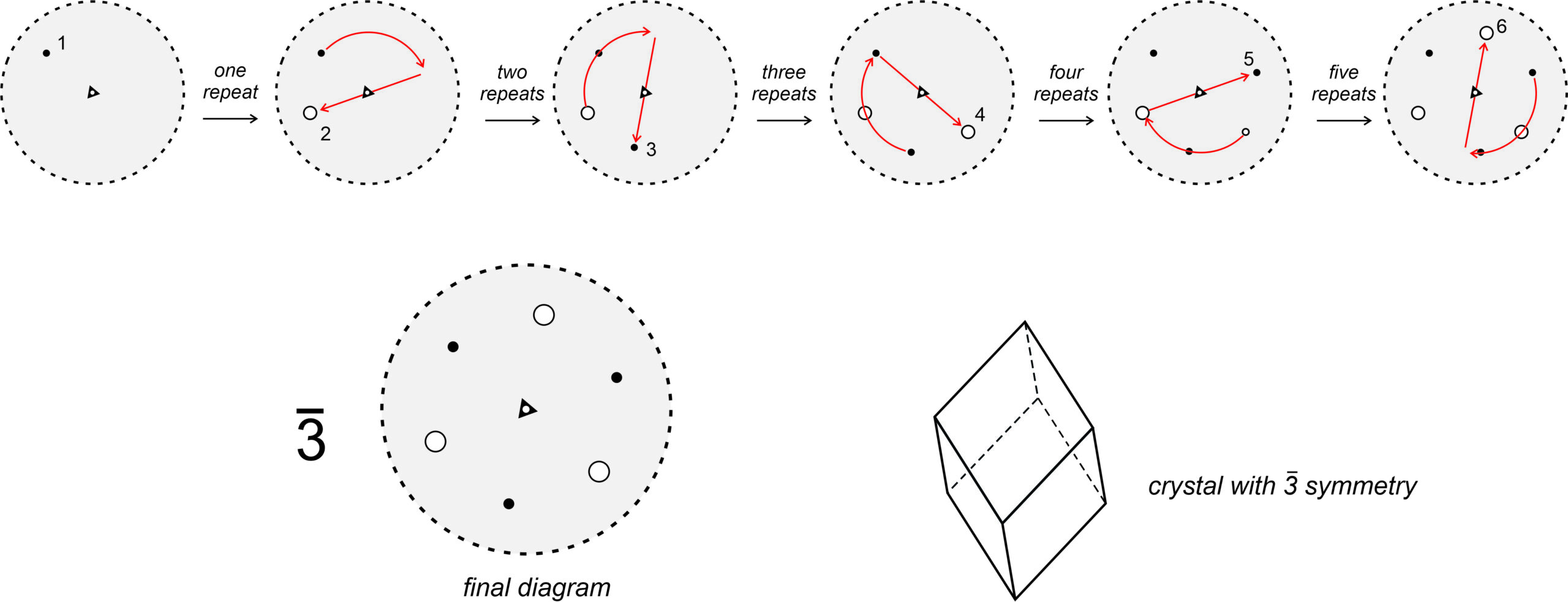
The drawing in the figure above shows a crystal that has a vertical 3 axis of symmetry. It also has mirror planes of symmetry, and 2-fold axes of symmetry (but they are hard to pick out in the drawing). This crystal form, called a rhombohedron, contains 3 crystal faces in its top half, and three in its bottom half, that are offset by 60^o with respect to each other — just as the three solid dots and three open circles are in the stereo diagram.

Figure 10.27, below, shows stereo diagrams for the different rotoinversion axes. Unlike 3, a 2, 4, or 6 operation is not equivalent to rotation and inversion operating separately, nor are they equivalent to proper 2-fold, 4-fold, or 6-fold rotation axes. But a 2 axis is equivalent to m; a 3 axis is equivalent to a 3-fold axis and an inversion center applied separately. A 6 axis is equivalent to a vertical 3-fold axis with a perpendicular mirror (in the plane of the page); it is equivalent to ³/_m. Note that 4 rotoinversion is the only rotoinversion operation completely distinct from other symmetry operations. Although it is called a rotoinversion axis, crystals with 4 symmetry have neither a 4-fold rotation axis nor an inversion center.

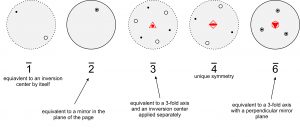
Figure 10.28 shows drawings of crystals with rotoinversion symmetry; they correspond to the stereo diagrams in Figure 10.27. Rotoinversion symmetry is often difficult to pick out in crystals and is more obvious in stereo diagrams.

Crystallographers rarely talk about 1 or 2 symmetry because it is simpler to talk about an inversion center or a mirror plane. References to 3, 4, and 6 are, however, normal, although we could describe two of them in other ways. The stereo diagrams in Figure 10.27 include (in red) the common symbols for 3, 4, and 6 at their centers.

10.3 From Points to Crystal Faces and Forms

In the preceding discussion, we talked about generic points and symmetry on stereo diagrams. And, we looked at some crystals with different symmetries. Now we will return to crystals and make the connection between crystal faces and stereo diagrams.

Crystallographers use the term form to describe a set of identically-shaped crystal faces related by symmetry. Use of this term is unfortunate, because most of us think of form as meaning shape. Further confusion arises because a single crystal may contain multiple forms, and a single form may have as many as 48 faces. Additionally, two crystals with identical forms may appear different if the forms are of different sizes. Nonetheless, the term form is firmly established in crystallography and unlikely to disappear. Crystallographers use various approaches to name forms, but A. F. Rogers’s system, published in 1935, is commonly used in the United States (Box 10-3).

Consider a crystal shaped like a shoe box (Figure 10.29). It contains three pairs of identical faces (opposite sides of the crystal). So, the crystal contains three forms. Figure 10.29 shows how orientations of the horizontal and vertical crystal faces may be shown on a stereo diagram. We depict the horizontal faces on the top and bottom of a crystal as solid and open dots, respectively, in the middle of the circle (drawings a and b).

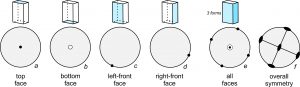
Vertical faces always plot as dots on the outside of the circle (drawings c and d) and are situated to show the aspect of the face (the direction the face is pointing). This crystal contains four vertical faces at 90^o to each other, and the crystal is oriented at an arbitrary angle. Drawing e shows all six of the faces on one diagram. The bull’s-eye at the center represents the top and bottom faces, and the dots on the circle represent the four vertical faces. Drawing f shows the overall symmetry. This crystal contains three perpendicular mirror planes and three perpendicular 2-fold axes.

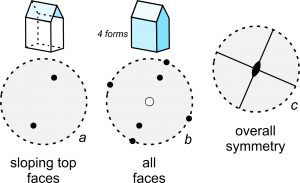
Many crystals contain sloping faces. If so, they plot as dots (or circles) that are somewhere between the center and the outside of a stereo diagram. And, we orient them to show their aspect. The house-shaped crystal seen in Figure 10.30 contains four forms – the same three that are in the shoe box we just saw plus a form composed of the two identical sloping faces on top. Black dots in drawing a show the sloping top faces. All faces are depicted in drawing b. Note that the bottom face is the only one that is an open circle. It is the only face below the plane of the page. The overall symmetry of this crystal (drawing c) is less than the symmetry of the shoe box described above. This crystal contains only two mirrors and a single 2-fold axis.

Earlier in this chapter, we introduced the idea of zones in crystals. In Figure 10.30b, five of the dots/circles representing faces are on a line (that is nearly vertical in the drawing). This means the faces are all parallel to a single horizontal direction; it means that together they form a zone.

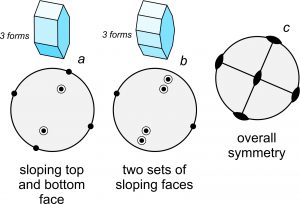
A crystal face that is almost, but not quite, horizontal will plot as a point near the center of a stereo diagram. A face that is almost vertical will plot close to the circle on the outside. And, faces with slopes of around 45^o will plot halfway between the center and the outside. So, the distance a point is from the centers describes the slope of the face. Figure 10.31 shows an example. Crystal a, containing three forms, has sloping faces on both the top and bottom of the crystal. Because the top faces are above the bottom faces, they appear as (two) bull’s-eyes within the circle. Crystal b (also three forms) contains two sets of sloping faces on the top and bottom, so the drawing contains four bull’s-eyes. The symbols closest to the outside of the circle represent the four faces that are almost vertical. The bull’s-eyes representing all the sloping faces indicate a zone; all faces in the zone are parallel to a single horizontal line. Drawing c shows the overall symmetry of both crystals; they contain three 2-fold axes and three mirrors. Although the two crystals in Figure 10.31 have a different number of faces, their symmetries are the same.

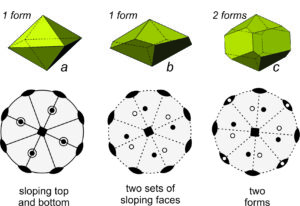
Figure 10.32 shows three more examples of crystals and stereo diagrams for each. Crystal a has a lot of symmetry – a 4-fold axis, four 2-fold axes and five mirror planes (four vertical and one horizontal). Crystal b also has a 4-fold axis and four 2-fold axes but contains no mirrors. Crystal c has the same symmetry as crystal b but contains four additional vertical prism faces. Unlike the previous figures, the stereo diagrams in Figure 10.32 show symmetry elements and face orientations (dots/circles) in the same diagram. This is standard practice but sometimes leads to a cluttered and confusing drawing, especially if points representing faces fall on top of symmetry elements.

When creating stereo diagrams, we orient a crystal so that rotation axes are vertical or horizontal (in the plane of the page or perpendicular to the page) if we can. This is what we did in Figure 10.32 and previous figures. Because mirror planes are generally parallel or perpendicular to rotation axes, mirrors too are horizontal or vertical most of the time.

If only looking at a stereo diagram, and not a crystal, we can rotate the diagram so that symmetry elements are mostly vertical or horizontal on the page. That means, for example, that if there is only one mirror plane present, we usually align it vertically and it appears as a vertical line in the diagram. But, if we wish to see side faces on a crystal, we usually rotate the crystal some arbitrary angle or the faces will not be visible. Suppose for example we view a cube perpendicular to one of its faces. We will only see a single square face – which is not very revealing. When we look at a cube from an oblique angle, we can see three faces and get a much better idea of its overall shape.

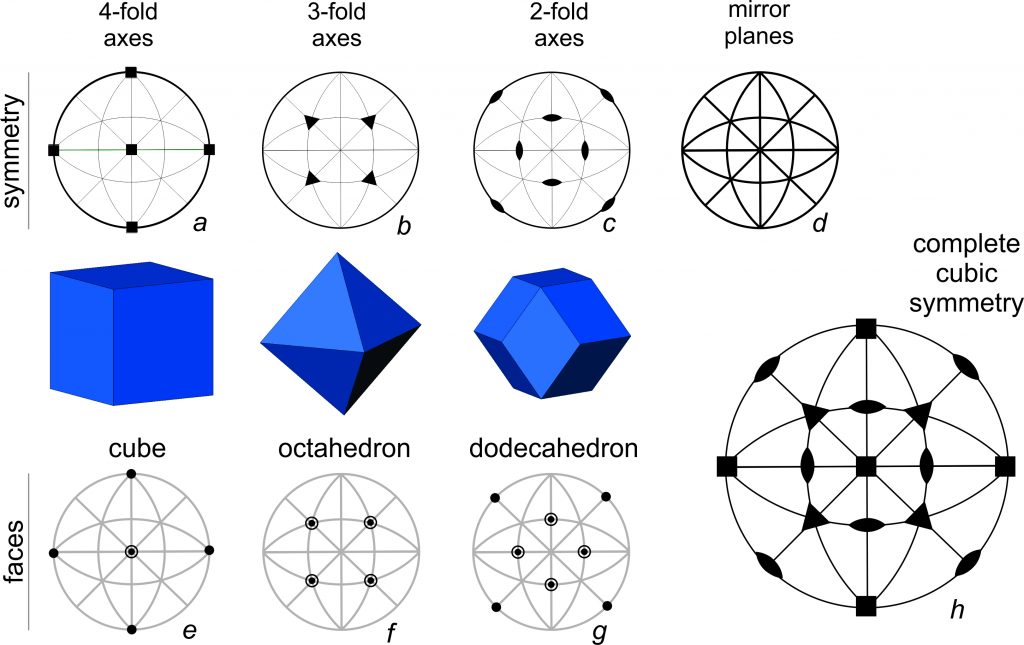
Earlier in this chapter, we observed that a cube and an octahedron have the same symmetry. It is worthwhile to revisit that idea using stereo diagrams. Consider the drawings of a cube, octahedron, and dodecahedron above in Figure 10.33. They have identical symmetry that includes 4-fold, 3-fold, and 2-fold rotation axes and many mirrors. We call this symmetry cubic symmetry. The large stereo diagram in drawing h shows all the elements of cubic symmetry.

In Figure 10.33, stereo diagram a above the cube shows the orientation of the 4-fold axes; they are perpendicular to the cube faces. Diagram b above the octahedron shows the orientation of the 3-fold axes; they are perpendicular to the octahedron faces. And, diagram c above the dodecahedron shows the orientation of the 2-fold axes are; they are perpendicular to the dodecahedron faces. Diagram d shows the orientations of the mirror planes; there is one perpendicular to each of the 4-fold and 2-fold rotation axes. The solid outer circle shows the horizontal mirror that goes through the center of each crystal. The four straight lines that intersect at the center of the diagram show vertical mirrors that bisect the crystal faces or that coincide with face edges. The four arc-shaped curves, halfway between the vertical and horizontal straight lines and the outer circle, show inclined mirrors.

10.3.1 Special Forms and General Forms

Diagrams e, f, and g in Figure 10.33 show stereo diagrams with points corresponding to the faces on a cube, octahedron, and dodecahedron. Cubes, octahedra and dodecahedra are special forms, and the points on the stereo diagram are called special points, because the faces/points coincide with symmetry elements. (For example, cube faces are perpendicular to 4-fold rotation axes.)

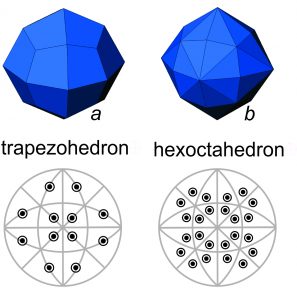
Besides the cube, octahedron and dodecahedron, other special forms have cubic symmetry. For example, Figure 10.34a shows a trapezohedron. As seen in the diagram beneath the crystal drawing, trapezohedron faces lie on (are perpendicular to) mirror planes. So, a trapezohedron is also a special form.

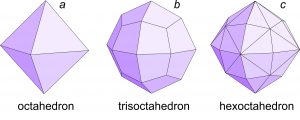
The hexoctahedron in Figure 10.34b, however is the general form that has cubic symmetry. It has the maximum number of faces for minerals with cubic symmetry (48) and the faces are neither parallel nor perpendicular to any symmetry elements (mirrors or rotation axes). No matter what the symmetry, the general form always has more faces than any special form.

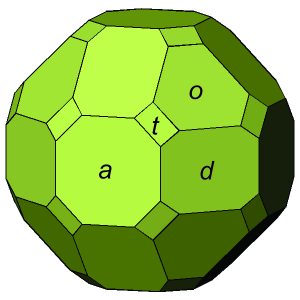
The examples of cubic crystals just seen (in Figures 10.33 and 10.34) contain a single form. But, cubic crystals commonly contain multiple forms. The crystal in Figure 10.35 is an example. It contains four forms: cube, octahedron, dodecahedron, and trapezohedron. This crystal contains four different shaped faces, one corresponding to each form; they are labeled with different letters. In all, the crystal has 38 faces. Yet, the symmetry of this crystal is the same as the crystals seen in the previous two figures.

10.3.2 Open Forms and Closed Forms

Figure 10.36 shows another example of form combinations. The figure contains four stereo diagrams depicting points related by ²/_m symmetry (a 2-fold axis with a perpendicular mirror). Drawings beneath each diagram show the same symmetry using crystal faces. The four faces of the prism (10.36a) are the general form; they are neither parallel nor perpendicular to the 2-fold axis or mirror plane. This form does not enclose space and so we call it an open form. (In contrast, the cubic forms we saw previously are all closed forms – they enclose a volume of space.) Because crystals cannot be open sided, additional crystal faces must terminate open forms. So, crystals with only one form must, of necessity, have a closed form.

Diagrams 10.36b and c show pinacoids. Pinacoids, which are pairs of parallel faces, are open forms. The pinacoids are special forms because the faces are perpendicular (10.36b) or parallel (10.36c) to the 2-fold axis. The pinacoids include two faces compared with the general form’s four. A combination of the general form and the two pinacoids produces a crystal with ²/_m symmetry (Figure 10.36d). Crystals with ²/_m symmetry always contain at least three forms. Compare this drawing with the shapes of the twinned feldspar crystals in Figure 10.37.

● Box 10-3 The Most Important Form Names The table below lists the most commonly used form names. This nomenclature derives from the work of A. F. Rogers’s in the 1930s. They are based on geometric shape or symmetry, but some of the names are unique to crystallography. Mineralogists group crystals into crystal systems based on common symmetry elements. We discuss the systems in detail later in this chapter. Most of the forms occur in more than one system, but the ones at the bottom of the table are exclusive to the cubic system. Figure 10.47 (later in this chapter) contains drawings of some of the cubic forms. The Most Common Form Names Open Forms pedions pinacoids prisms pyramids domes sphenoids single face two parallel faces 3, 4, 6, 8, or 12 faces parallel to a common line 3, 4, 6, 8, or 12 sloping faces that meet at a point two nonparallel faces related by a mirror two nonparallel faces related by a 2-fold axis Closed forms scalenohedrons trapezohedrons disphenoids dipyramids rhombohedrons 8 or 12 scalene triangle faces 6, 8, or 12 trapezoid faces four nonequilateral triangular faces two 3-, 4-, 6-, 8-, or 12-sided pyramids six rhomb-shaped faces Cubic forms (closed) tetrahedrons cubes (hexoctahedrons) octahedrons dodecahedrons pyritohedrons tetartoids diploids and gyroids four equilateral triangular faces six square faces eight equilateral triangular faces 12 rhomb-shaped faces 12 irregular 5 sided faces 12 five-sided faces 24 five-sided faces . In form names, the suffix –hedron means face. Prefixes describe the shape of faces: scaleno– (scalene triangle), rhombo– (rhomb shaped), and trapezo– (trapezoid shaped). We use descriptive modifiers to make the basic names more specific. For example, prisms may be hexagonal-, tetragonal-, orthorhombic- or monoclinic-prisms (having six, four, four, and two faces, respectively). Thus, the modifiers hexagonal, tetragonal, and orthorhombic identify the number of faces. For example, Figure 10.38a (below) shows a tetragonal (four faces) prism. We use these same modifiers for pyramids. For example, a hexagonal pyramid has six sides, while a tetragonal pyramid has only four (Figure 10.38b). An orthorhombic pyramid has four sides but they are of two different shapes. 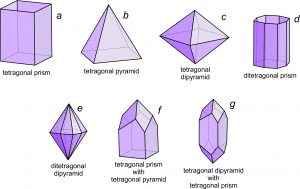We can add a further modifying prefix to the word pyramid. The prefix di– indicates that there are two equivalent pyramids related by a mirror plane. Figure 10.38c is a tetragonal dipyramid. The prefixes di-, tris-, tetra-, and hex– describe a doubling, tripling, and so on, of faces. If each of the four sides on a tetragonal prism is split down the middle to produce two faces we get a ditetragonal prism (Figure 10.38d). And, if each face on a tetragonal pyramid is split into two, we get a ditetragonal pyramid (Figure 10.38e). These different forms can combine in a single crystal; Figures 10.38f and g show some combinations. Similarly, we can replace each face on an octahedron (Figure 10.39a) by three faces to get a tetragonal trisoctahedron, also called a trapezohedron (Figure 10.39b). There is another kind of of trisoctahedron (not shown) that contains triangular faces. And if each face on an octahedron is replaced by six faces, the result is a hexoctahedron (Figure 10.39c).

10.4 Combinations of Symmetry Elements: Point Groups

symmetry operators

i m = 2 = 1/m 1 2 3 4 6 3 4 6 = 3/m 2/m 4/m 6/m

Because some symmetry operators are redundant, we do not need them all to describe the symmetry of crystals. By convention, crystallographers use the 13 operators listed in the table seen here. In mathematical terms, these 13 are sufficient to describe symmetry in any crystal.

These symmetry operators can combine, so more than one can be present in a crystal. But, the number of possible combinations is limited for two reasons. First, some combinations lead to other symmetry. Second, some combinations are contradictory and thus impossible.

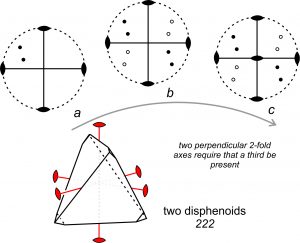
Consider, for example, a crystal that has two 2-fold axes of symmetry that intersect at 90^o , as depicted in Figure 10.40. If we start with dots representing two faces (diagram a), application of the symmetry operators produces six more dots/faces (diagram b). Four of the faces are above the page and four below. Diagram b reveals that a third 2-fold axis is perpendicular to the original two, shown by a lens shape at the center of diagram c. Thus, we see that all objects that have two perpendicular 2-fold axes of symmetry must have a third 2-fold axis. It does not matter which two 2-fold axes we choose initially; the third must be there. Figure 10.40 reinforces what we concluded earlier – that symmetry operators operate on each other.

The symmetry depicted in Figure 10.40 consists of three mutually perpendicular 2-fold axes. We use the shorthand notation 222 to describe this symmetry. The drawing in the bottom of Figure 10.40 is only one of many possible crystal shapes that have 222 symmetry. The three 2-fold axes (shown in red) pass through the centers of edges of the crystal. Four faces related by 222 symmetry make up a disphenoid. The crystal depicted contains two forms; both are disphenoids. The four faces of one form are, however, quite small and just show at the corners of the crystal.

We call distinct combinations of symmetry, such as 222, point groups. So, the crystal in Figure 10.40 belongs to point group 222. Figure 10.36 showed a crystal that belonged to a different point group, ²/_m. Point groups describe symmetry around a point in the center of a crystal, and thus they relate the points in a stereo diagram to each other. The word group is used because we may treat the principles of symmetry using mathematical group theory. The terms operator and operation also derive from group theory. In group theory, the 13 operators listed in the table above form a basis, which means we need no other operators to describe all possible manifestations of symmetry.

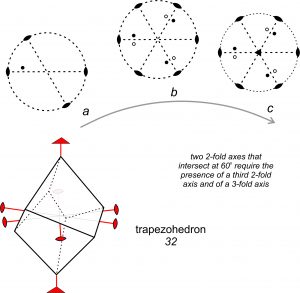
Figure 10.41 shows another example of symmetry operators acting on each other. Two 2-fold axes intersect at 60^o (diagram a). Starting with one point and applying the symmetry operators, we soon generate five more equivalent points (diagram b). Examination of the resulting pattern shows that a third 2-fold axis lies at 60° to the first two. Additionally, a 3-fold axis (shown by a triangle at the center of the diagram) is perpendicular to the two folds (diagram c). Another way of looking at the symmetry in Figure 10.41 is to notice that the 3-fold rotation axis acts on the 2-fold axes. It requires that if one 2-fold axis of symmetry is present, two others must be present as well, and that the three are related by angles of 120°. The point group for this symmetry is designated 32. The drawing in the bottom of Figure 10.41 shows a crystal that has 32 symmetry. It is a trapezohedron, named after the shapes of its faces.

In Figure 10.40 we showed that two perpendicular 2-fold axes required the presence of a third mutually perpendicular one. In Figure 10.41, we showed that if two 2-fold axes intersect at 60°, another 2-fold and a 3-fold will also be present. Similarly, if we start with a 4-fold axis and one perpendicular 2-fold, we will find other 2-folds perpendicular to the 4-fold and at 45° to each other. If we start with a 6-fold axis and a perpendicular 2-fold, we will find six 2-fold axes in all.

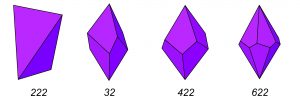
Figure 10.42 shows drawings of crystals belonging to point groups 222, 32, 422, and 622. Note that mirror planes are absent in all four cases. The top and bottom of the crystals do not mirror each other, and the crystal faces do not have mirror planes down their centers or edges (or else an m would be included in the symbol for the point group). The four examples point out that symmetry operators cannot combine in random ways. The presence of two rotation axes requires a third and perhaps more. We can also show that a combination of a rotation axes and a mirror, at angles other than 0° or 90° to each other, requires other rotation axes to be present. Seeing symmetry on the complicated crystal drawings in Figure 10.42 is difficult. (That’s why we have stereo diagrams!) A better way to examine symmetry of crystals is to study models in the laboratory.

Before leaving this discussion about the way symmetry combines to produce other symmetry, let’s consider one more example. Figure 10.43a shows points related by a 4-fold rotation axis. We can add a horizontal mirror (shown by the solid outer circle) to produce the points shown in diagram b. Adding a vertical mirror produces diagram c. And, in diagram c, we see that this is equivalent to symmetry that includes a 4-fold axis and two different kinds of 2-fold axes (shown in diagram d). All the rotation axes are perpendicular to mirror planes. This is point group ⁴/_m²/_m²/_m.

10.4.1 Special Angles and General Angles

Angles such as 30°, 45°, 60°, 90°, or 120° are called special angles. They all divide evenly into 360°. We call nonspecial angles general angles. In the examples in Figure 10.43, and others considered previously, we started with rotation axes and mirror planes that intersected at special angles. Suppose we start with axes or mirrors that intersect at general angles. What will be the result?

The first diagram in Figure 10.44 shows two intersecting 2-fold axes and three points related by them. The angle between the axes is small and does not divide evenly into 360°. It is a general angle. We may apply the 2-fold axes to each other to generate more 2-fold axes and points, moving around the diagram in a stepwise manner as shown. We could do this forever, continuing around the circle indefinitely, because the new axes and points we generate will never coincide with others already present. When we continue this operation all the way around the circle, we will not end back where we started. So, the number of 2-fold axes becomes infinite, and an infinite-fold axis of symmetry must be perpendicular to the plane of the page. This is equivalent to the symmetry of a circle. Since crystals consist of a discrete number of faces (and atomic arrangements consist of a discrete number of atoms), we know that infinite symmetry is not possible. We may therefore conclude that if crystals have two 2-fold axes, they must intersect at a special angle so that they are finite in number.

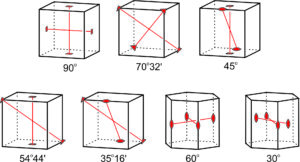
The preceding discussion suggests that rotation axes only combine in a limited number of ways. In fact, angles between rotation axes are limited to the seven depicted in Figure 10.45. We have already seen examples of each. These drawings are of a cube and a hexagonal prism, but angles between rotation axes in crystals of other shapes are limited to the same seven values. The possible angles between rotation axes are all special angles. If we carried out the exercise, we would find that in crystals with both rotation axes and mirror planes, the angles between the rotation axes and the mirror planes are limited to only a few special angles as well. Otherwise, we have infinite symmetry. In most crystals the angles are 0° (the rotation axis lies within the plane of the mirror) or 90° (the rotation axis is perpendicular to the mirror).

10.5 Point Groups and Crystal Systems

The 32 Point Groups
system	point group	general form
cubic	4/m32/m 432  43m 2/m3 23	hexoctahedron gyroid hextetrahedron diploid tetartoid
hexagonal	6/m2/m2/m 622 6mm 6m2 6/m 6 6	dihexagonal dipyramid hexagonal trapezohedron dihexagonal pyramid ditrigonal dipyramid hexagonal dipyramid hexagonal pyramid trigonal dipyramid
trigonal	32m 32 3m 3 3	hexagonal scalenohedron trigonal trapezohedron ditrigonal pyramid rhombohedron trigonal pyramid
tetragonal	4/m2/m2/m 422 4mm  42m 4/m 4 4	ditetragonal dipyramid tetragonal trapezohedron ditetragonal pyramid tetragonal scalenohedron tetragonal dipyramid tetragonal pyramid tetragonal disphenoid
orthorhombic	2/m2/m2/m 222 mm2	rhombic dipyramid rhombic disphenoid rhombic pyramid
monoclinic	2/m 2 m	monoclinic prism sphenoid dome
triclinic	1 1	pinacoid pedion

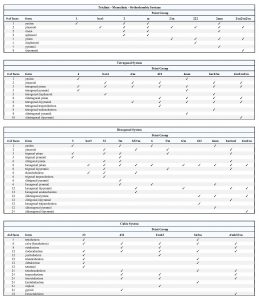
For the reasons discussed above, symmetry operators can combine in a surprisingly small number of ways. Only 32 combinations are possible; they represent the only combination of symmetry elements that crystals, or arrangements of atoms, can have. This leads to the division of crystals into 32 distinct point groups, also sometimes called the 32 crystal classes, each having their own distinct symmetry. They are listed in the table here. We can make drawings of crystal shapes with all 32 possible symmetries, but some of them are not represented by any known minerals. Chapter 14 in this book describes 180 of the most common minerals. They fall into 24 of the possible 32 crystal classes. About a third of them are monoclinic.

Box 10.4 below discusses in more detail the symbols we use to describe the symmetry of different point groups. In some mineralogy texts, the hexagonal and trigonal systems are grouped into a hexagonal crystal family. This is because possible lattices for each system were derived by stacking hexagonal plane nets (discussed more fully in the next chapter).

The column on the right in the table lists the names of the general forms for each point group. Sometimes crystallographers use these form names as names for the crystal classes. Although the expression point group refers only to symmetry, and crystal class refers specifically to the symmetry of a crystal, the semantic difference is subtle and the two phrases are often used interchangeably. Some of the general forms, indicated by blue text, are open forms that must combine with other forms to make a crystal, like the forms we saw in Figure 10.36.

Each of the 32 crystal classes belongs to one of the seven crystal systems (cubic, hexagonal, trigonal, orthorhombic, tetragonal, monoclinic, and triclinic, listed in the table) based on common symmetry elements. Crystals are made of unit-cell building blocks that have different shapes for each of the systems. Because cubic unit cells have the most symmetry possible, cubic crystals may have lots of symmetry. At the other extreme, triclinic unit cells have shapes equivalent to a squashed box with no edges of equal length and no 90^o corners. This is why the most symmetry a triclinic crystal can have is an inversion center (1).

All cubic crystals contain more than one 3-fold or 3 rotation axes. All hexagonal crystals contain a single 6-fold or 6 rotation axis. All trigonal crystals contain a single 3-fold or 3 rotation axis. All tetragonal crystals contain a single 4-fold or 4 rotation axis. All orthorhombic crystals contain three perpendicular 2-fold rotation axes (with or without perpendicular mirrors) or two mirrors and one 2-fold axis. They contain no 3- or 4-, or 6-fold axes. Monoclinic crystals contain one 2-fold axis, one mirror, or one 2-fold axis with a perpendicular mirror. Triclinic crystals may have an inversion center of symmetry; no other symmetry is possible.

● Box 10-4 Hermann-Mauguin Symbols to Designate Point Groups The symbols used in this book are based on notations developed by C. H. Hermann and C. V. Mauguin in the early 1900s. They have been used by most crystallographers since about 1930. One, two, or three symbols describe a point group; they combine in different ways for different systems. crystal system possible first symbol possible second symbol possible third symbol example of a point group cubic hexagonal trigonal tetragonal orthorhombic monoclinic triclinic 4, 4/m, 4, 2, 2/m 6, 6/m, 6 3, 3 4, 4/m, 4 2, m,2/m 2, 2/m, m 1, 1 3, 3 2, 2/m, m 2, 2/m, m 2, 2/m, m 2, 2/m, m blank blank 2, 2/m, m 2, 2/m, m 2, 2/m, m 2, 2/m, m 2, 2/m blank blank  43m 6/m2/m2/m 32 422 mm2 2/m 1 Numbers in the symbols refer to rotation axes of symmetry; a bar over a number indicates a rotoinversion axis. Mirrors, designated by m, are perpendicular to an axis if they appear as a denominator (for example, 4/m), and parallel to an axis otherwise. When articulating the symbols, they are pronounced just as if they were typographical characters. 4/m32/m, for example, is read “four over em, bar three, two over em.” For cubic point groups, the first symbol describes three mutually perpendicular principal symmetry axes, oriented perpendicular to cube faces (if cube faces are present). The second describes four axes oriented at angles of 54°44′ to the principal axes. They correspond to the body diagonals of a cube, a diagonal from a corner through the center to the opposite corner. The third symbol, if present, describes six 2-fold axes or mirror planes oriented at angles of 45° to the principal axes. They correspond to edge diagonals of a cube, diagonals from the center of edges through the center of the cube to the opposite edge. For hexagonal point groups, the first symbol describes the single principal axis. The second, if present, describes three secondary rotation axes oriented at 120° to each other and perpendicular to the principal axis, or three mirror planes oriented at 120° to each other and parallel to the principal axis. The third symbol, if present, represents mirror planes or 2-fold axes oriented between the secondary axes. For tetragonal point groups, the first symbol represents the principal axis. The second, if present, represents two secondary axes perpendicular to each other and to the principal axis, or two mirror planes oriented at 90° to each other and parallel to the principal axis. The third represents axes or mirror planes between the secondary axes. Only three orthorhombic point groups are possible. Point group 222 has three mutually perpendicular 2-fold axes. Point group mm2 has one 2-fold axis with two mutually perpendicular mirror planes parallel to it. Point group 2/m2/m2/m has three perpendicular 2-fold axes with mirror planes perpendicular to each. For monoclinic point groups, only one symmetry element is included in the Hermann-Mauguin symbols because the only possible symmetries are a 2-fold axis, a mirror, or a 2-fold axis with a mirror perpendicular to it. Similarly, for triclinic crystals, the only possible point groups are 1 and 1.

space

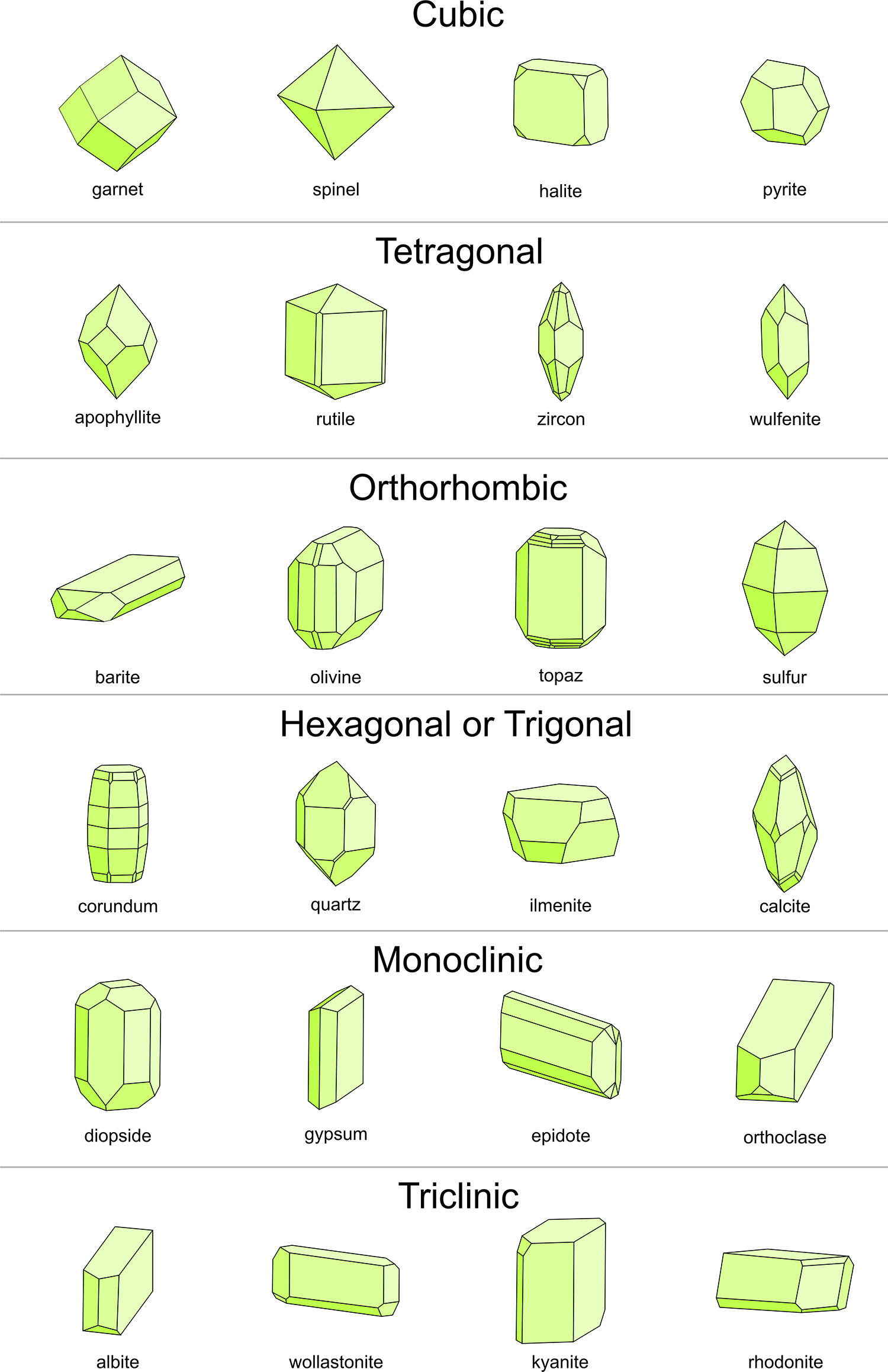
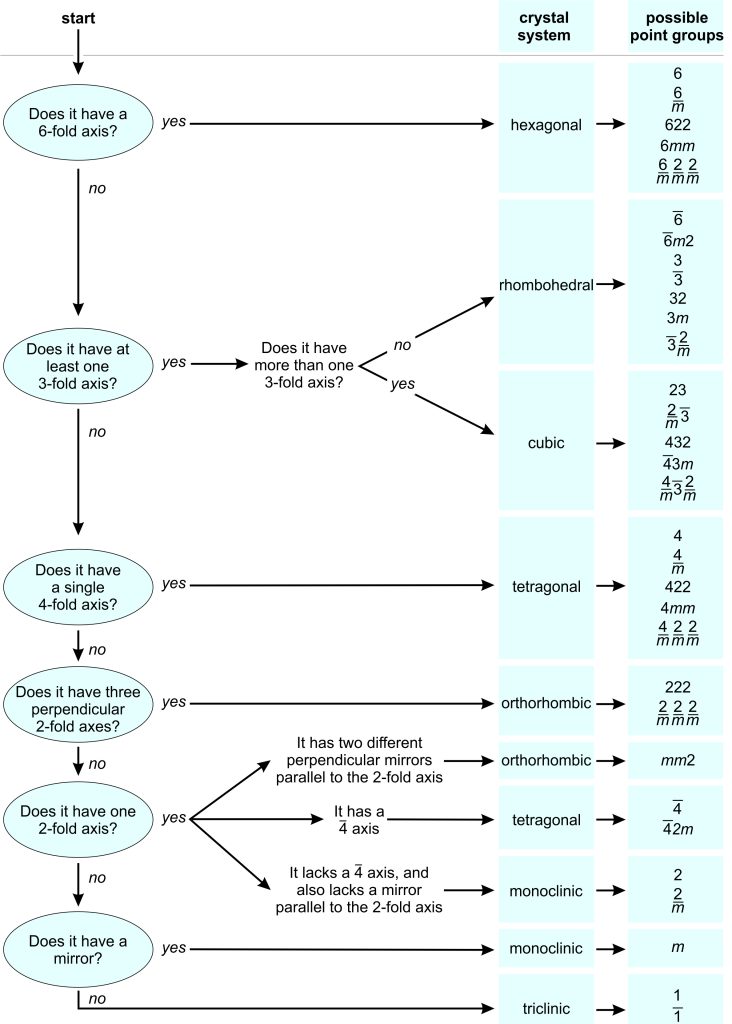
Figure 10.46 above shows representative drawings for common minerals that belong to each crystal system, and Box 10-5 contains a flow chart that can be used to determine the crystal system and point group of many well-formed crystals. But, sometimes determining the point group and system of a crystal, especially for imperfect crystals, is quite difficult or impossible. Overall, it is much easier to see symmetry in crystals with high symmetry (e.g., cubic or hexagonal crystals) than in crystals with lesser symmetry. Distinguishing monoclinic from triclinic crystals, for example, can be very difficult. Yet, crystals that belong to a given system share characteristics, so we can sometimes identify the crystal system quite quickly (especially for crystals with lots of symmetry). For example, as seen in Figure 10.46:

• cubic crystals tend to be equant (equidimensional)
• multiple perpendicular faces are common in cubic, tetragonal and orthorhombic crystals
• hexagonal and tetragonal crystals may contain prism faces parallel to a long dimension
• hexagonal crystals may contain prism faces that intersect at 120^o
• trigonal crystals typically show 3-fold symmetry
• monoclinic crystals are commonly tabular (thin in one dimension)
• orthorhombic crystals often have an overall shoe-box shape

For further discussion of the similarities and differences of crystals belonging to different crystal systems, check out the video linked below:
blank▶️ Video 10-4: A closer look at different crystal systems (6 minutes)

Minerals belong to all seven crystal systems. About 10% of the common minerals are cubic, 10% are tetragonal, 10% are triclinic, 20% are hexagonal or trigonal; the remainder are 25% orthorhombic and 25% monoclinic. Within each system, different point groups have different amounts of symmetry. Most natural crystals fall into the point group with the highest symmetry in each system. Few belong to the point groups of lowest symmetry.

● Box 10-5 Flow Chart for Determining Crystal System and Point Group

10.5.1 Forms and Point Groups

On the basis of the relative positions of crystal faces and possible symmetries, crystallographers have distinguished 48 distinctly different forms. Figure 10.47, below, shows 28 examples. Symmetry is listed for each, but many of the forms can occur in crystals of more than one point group because they can be both general forms and special forms. For example, a tetragonal pyramid is the general form for crystals with symmetry 4. It is a special form for crystals with symmetry 4mm. A rhombohedron is the general form for point group 3, but is a special form in point groups 32 and 3. And, cube faces may be present in crystals with symmetry of any of the cubic point groups (23, 432, ²/_m3, 43m, or ⁴/_m3²/_m). The table below Figure 10.47 lists the possible forms in each of the 32 point groups.

We should emphasize that although only 48 possible forms exist, they can have an infinite number of sizes and shapes. A disphenoid, a form consisting of four faces, may be tall and skinny or short and wide. Nevertheless, it is still a disphenoid. And Figures 10.36 and 10.37 show a crystal that contains two different pinacoids with different shaped faces.

Forms retain their names, even if truncated by other forms. Consider the complex crystal in Figure 10.35. It contains four forms: cube, octahedron, trapezohedron, and dodecahedron. The faces corresponding to the forms do not have the same shape as they would if they were the only form in the crystal. And, in many other figures (e.g., Figures 10.28, 10.32, 10.38), pyramids and prisms truncate each other.

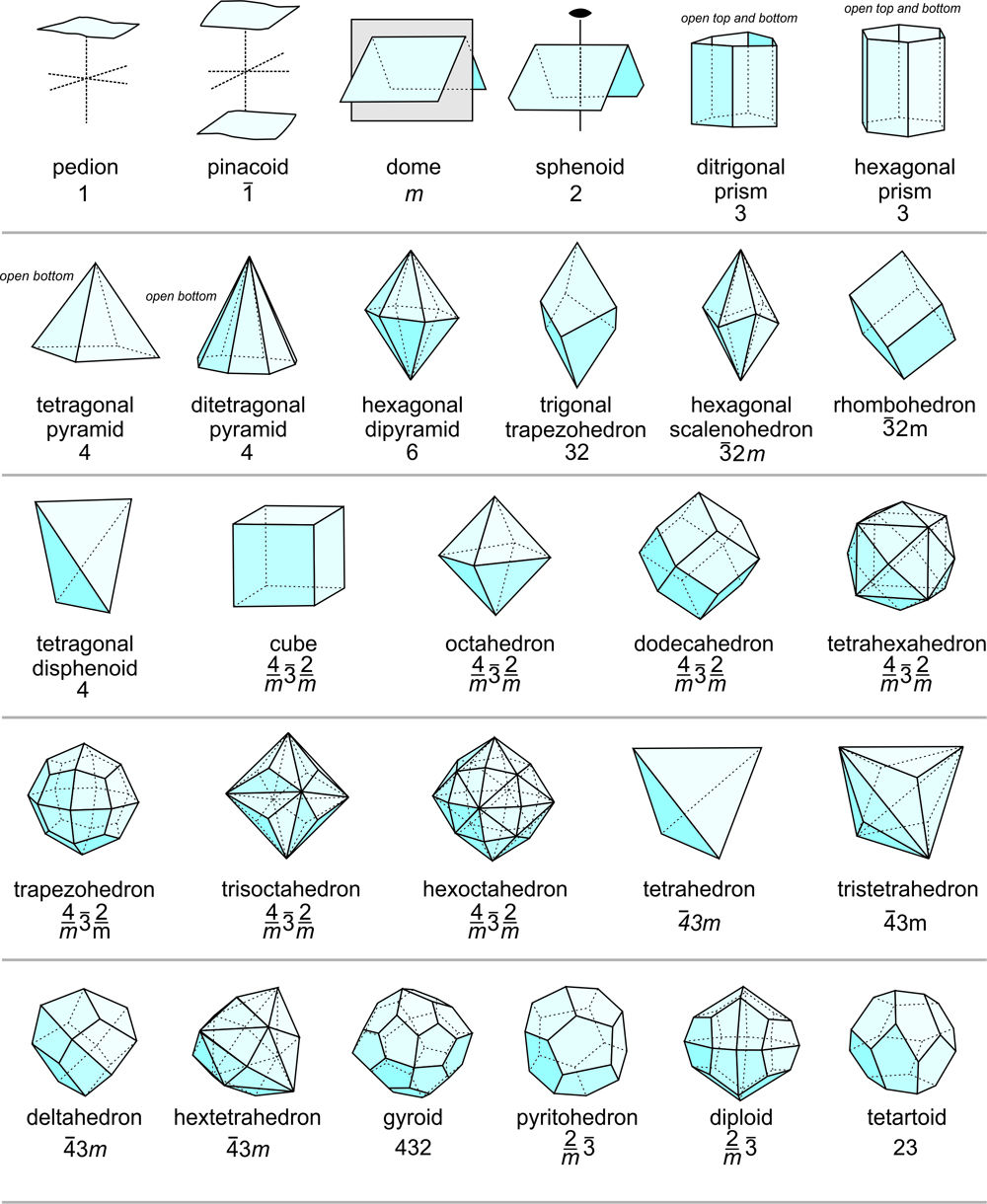
Possible Forms in Different Point Groups

Most mineral crystals contain more than one form, leading to a large but limited number of possible combinations. The number of possible combinations is limited because the shape and symmetry of crystal faces depend on a crystal’s point group which, in turn depends on the atomic arrangement within the crystal. For example, if the atoms within a crystal are not arranged in hexagonal patterns, forms may not have hexagonal symmetry. Similarly, a crystal may not develop a cubic form unless atoms are in a cubic arrangement. Thus, certain forms never coexist in crystals, while others are often found together. Because the forms present in particular crystals depend on atomic arrangements, they are generally consistent for a given mineral. Uncertainty arises, however, because some minerals can have crystals with several different combinations of forms, and it is not always clear why one develops instead of another. However, if we know the point group of a crystal, we can look in the table above to see which forms may be present.

10.5.2 Characteristics of Crystals Belonging to the Different Crystal Systems

10.5.2.1 Cubic System

The cubic system is also called the isometric system. Crystals have high symmetry, all having four 3-fold or four 3 axes. Some have three 4-fold axes as well, and some have 2-fold axes or mirror planes. Cubes and octahedra are examples of forms belonging to the cubic system, but other forms belong to the cubic system, too. We saw some special forms (cube, octahedron, dodecahedron, and trapezohedron) and the general form, a hexoctahedron, earlier in this chapter.

The three photos below are crystals belonging to the cubic system. Figure 10.48 shows a dodecahedral garnet. It has symmetry ⁴/_m3²/_m; a dodcahedron is a special form in that point group. Figure 10.49 shows a pyrite crystal with 5-sided faces. The form is called a pyritohedron. Pyrite has symmetry ²/_m3, and the pyritohedron is the general form in the ²/_m3 point group. Figure 10.50 shows pyrite octahedra. Some small cube faces are present, too. Like the dodecahedral garnet, these crystals have symmetry ⁴/_m3²/_m. And like the dodecahedron, octahedra and cubes are special forms in the class.

Crystals of the cubic system may have many different and complex shapes, but all tend to be equant, meaning they are approximately equidimensional. Often the crystals contain only one or two forms.

We saw other examples of minerals whose crystals belong to the cubic system in earlier chapters:
•pyrite in Figure 3.3 (Chapter 3)
•halite in Figure 3.2 (Chapter 3)
•garnet in Figure 3.6 (Chapter 3)
•fluorite in Figure 3.69 (Chapter 3), Figure 4.37 (Chapter 4)
•galena in Figure 9.34 (Chapter 9)

10.5.2.2 Hexagonal and Trigonal Systems

Hexagonal crystals have a single 6-fold, or 6 axis. Trigonal crystals contain a single 3-fold or 3 axis. Crystals with more than one 3-fold or 3 axis belong to the cubic system. No crystals have more than one 6-fold or 6 axis. Crystals in either system may also have 2-fold axes and mirror planes. Because they have one direction that is different from others, hexagonal crystals are often prisms of three or six sides terminated by pyramid faces. Other forms, including scalenohedron and rhombohedron, are also common in both the hexagonal and trigonal systems.

Figure 10.51 shows a crystal of hanksite, a rare sodium-potassium evaporite mineral that has symmetry ⁶/_m. The hexagonal symmetry is reminiscent of apatite crystals. Figure 10.52 shows prismatic tourmaline crystals. They have symmetry 3m. Figure 10.53 shows one large, and several small, calcite scalenohedra. Calcite has symmetry 32m, but calcite crystals have many common forms and come in many shapes.

We saw other examples of minerals whose crystals belong to the hexagonal or trigonal systems in earlier chapters:
•quartz in Figure 1.8 (Chapter 1)
•beryl in Figure 1.12 (Chapter 1), Figure 4.1 (Chapter 4), Figure 6.89 (Chapter 6), Figure 9.60 (Chapter 9)
•tourmaline in Figure 4.13 (Chapter 4) and 6.22 (Chapter 6)
•calcite in Figure 3.1 (Chapter 3)
•molybdenite in Figure 3.40 (Chapter 3)
•graphite in Figure 3.78 (Chapter 3)
•ilmenite in Figure 9.55 (Chapter 9)
•chabazite in Figure 7.56 (Chapter 7)

Note that micas and other sheet silicate minerals sometimes appear to be hexagonal. For example, look at the biotite crystals in Figure 6.62, the lepidolite in Figure 6.66, and the clinochlore in Figure 6.69. In two dimensions they appear hexagonal, but if you could see the third dimension clearly it would be apparent that they are not. Most sheet silicates are monoclinic. Tourmaline, too, often appears hexagonal but a close look reveals that the crystal cross sections are 6-sided but are not true hexagons.

10.5.2.3 Tetragonal System

All tetragonal crystals have one 4-fold or one 4 axis of symmetry; crystals that have more than one 4-fold or 4 axis must belong to the cubic system. Tetragonal crystals may also have 2-fold axes and mirror planes. As with the crystals in the hexagonal system, tetragonal crystals are often combinations of prisms with other forms. Figure 10.54 shows a green apophyllite crystal from Bombay, India. It has prominent tetragonal prism and tetragonal pyramid faces. Compare this with the other photo of apophyllite earlier in this chapter (Figure 10.13). The apophyllite in Figure 10.54 is on top of stilbite. Apophyllite (which is a sheet silicate) usually occurs with zeolites such as stilbite (which is a monoclinic framework silicate). We find these minerals most commonly as secondary minerals in vugs and pockets in basalt.

Figure 10.55 show tetragonal vesuvianite crystals with both prism and pyramid faces. Both apophyllite and vesuvianite have symmetry ⁴/_m²/_m²/_m. Figure 10.56 shows another tetragonal mineral, wulfenite, forming thin square orange crystals. Wulfenite crystals have symmetry ⁴/_m.

10.5.2.4 Orthorhombic System

Crystals in the orthorhombic system have either three perpendicular 2-fold axes, two perpendicular mirror planes paralleling a 2-fold axis, or three perpendicular 2/m axes. A shoebox shape is an excellent example, but many shapes and forms are possible. The sulfur crystal shown in Figure 10.57, the topaz in Figure 10.58, and the barite in Figure 10.59 all have symmetry 2/m2/m2/m. The crystal with disphenoids in Figure 10.40, earlier in this chapter, is also orthorhombic and belongs to point group 222. Sometimes orthorhombic crystals may be rather equant but they are often quite tabular, like the barite crystals seen in the opening photo of this chapter (Figure 10.1) and here in Figure 10.59.

10.5.2.5 Monoclinic System

A single 2-fold axis, a single mirror, or a 2-fold axis perpendicular to a mirror characterize crystals in the monoclinic system. In the simplest case, monoclinic crystals may appear as shoe boxes distorted in one direction so that two faces are not rectangles. The symmetry may be hard to see because monoclinic crystals often comprise many different forms. Figure 10.60 shows gypsum, Figure 10.61 shows a large orthoclase crystal from the Jarilla Mountains, southern New Mexico, and Figure 10.62 shows a cluster of heulandite crystals (Ca-Na zeolite) from Maharashtra, India. All these monoclinic crystals have symmetry 2/m but it is hard to discern in the heulandite crystals.

We saw other examples of minerals whose crystals belong to the monoclinic system in earlier chapters:
• twinned gypsum Figure 4.39 (Chapter 4)
• twinned orthoclase in Figure 4.41 (Chapter 4)
• augite in Figure 6.78 (Chapter 6)

10.5.2.6 Triclinic System

Triclinic crystals have no symmetry greater than an inversion center. The photos below show three examples: albite from Tuscany, Italy (Figure 10.63), amblygonite from Brazil (Figure 10.64), and rhodonite from Brazil (Figure 10.65). The photo of albite also contains minor amounts of black tourmaline and quartz. These crystals all have symmetry 1, equivalent to an inversion center, and no more. It appears that the albite crystal might have a vertical mirror and so, perhaps, be monoclinic. But albite, like all plagioclase, is triclinic. In contrast with plagioclase feldspars, K-feldspar is monoclinic at high temperature (sanidine, orthoclase) and triclinic at low temperature (microcline).

We saw other examples of feldspar crystals in the triclinic system in earlier chapters:
•albite in Figure 6.37 (Chapter 6)
•anorthite in Figure 6.38 (Chapter 6)blank line

blank line

●Figure Credits Uncredited graphics/photos came from the authors and other primary contributors to this book. 10.1 Barite crystals, Carlesmillan, Wikimedia Commons 10.7 Lion, Clément Bardot, Wikimedia Commons 10.13 Apophyllite on stilbite and calcite, rosellminerals.com 10.16 A hexagonal prism terminated by pyramid faces, Géry Parent, Wikimedia Commons 10.37 Twinned orthoclase, skywalker, Wikimedia Commons 10.48 Pyrope, Géry Parent, Wikimedia Commons 10.49 Pyrite , Robert M. Lavinsky, Wikimedia Commons 10.50 Pyrite, mindat.org 10.51 Hanksite , Robert M. Lavinsky, Wikimedia Commons 10.52 Tourmaline, Géry Parent, Wikimedia Commons 10.53 Calcite, Robert M. Lavinsky, Wikimedia Commons 10.54 Apophyllite , Robert M. Lavinsky, Wikimedia Commons 10.55 Vesuvianite , Robert M. Lavinsky, Wikimedia Commons 10.56 Wulfenite , Marie-Lan-Taÿ-Pamart, Wikimedia Commons 10.57 Sulfur, Nevada-Outback-Gems.com 10.58 Topaz, Robert M. Lavinsky, Wikimedia Commons 10.59 Barite, mediastorehouse.com 10.60 Gypsum, fineartamerica.com 10.61 Orthoclase, ebay.com 10.62 Heulandite, Didier Descouens, Wikimedia Commons 10.63 Albite, Sarah Sutcowsky, pinterest.com 10.64 Amblygonite, fabreminerals.com 10.65 Rhodonite, Robert M. Lavinsky, Wikimedia Commons Video 10-1: Symmetry of crystals, Keith Putirka, YouTube Video 10-2: Mirror planes, Keith Putirka, YouTube Video 10-3: Inversion centers, Keith Putirka, YouTube Video 10-4: A closer look at crystal systems, Keith Putirka, YouTube